Answer: The reasonable range is the set of real numbers between 0 and 14.5 inclusive.
The function
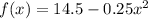 is used to model the curve of a train tunnel,
is used to model the curve of a train tunnel,
The graph of function will be inverted U shaped figure.
So the range will be less than y coordinate of vertex
Lets find the vertex
formula to find x co-ordinate of vertex is

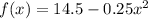 , a=-0.25, b=0
, a=-0.25, b=0
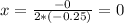
Now we plug in 0 for x in f(x)
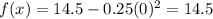
The y co-ordinate of vertex is 14.5
We know x axis represents the ground. The height of the curve cannot be negative. So, the curve of a tunnel starts at 0. The range is from 0 to 14.5
We cannot take only whole numbers for y.
So, The reasonable range is the set of real numbers between 0 and 14.5 inclusive.