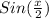Question

The graph of f(x) = sin(x) is stretched until it has a period of 4align='absmiddle'. This new graph is described by which of the following functions?

f(x) = sin(x)
f(x) = sin(x)
f(x) = sin(2x)
f(x) = sin(4x)

Answer 1

`Sin((x)/(2))`

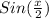
Explanation:

The period of a sine function is the angle measurement in radians in which the graph completes one complete cycle.

The period of a sin functio in its standard form is
`2\pi`

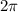
When the graph is stretched on x axis to a level that it now comletes one complete cycle in
`4\pi`, there are changes in the angle whose sine has been taken

Which is given by the rule which says

The period of
`Sin((x)/(n))=2n\pi`

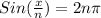
Hence the function having
`2*2\pi` as its period, will be
`Sin((x)/(2))`

Answer 2

We don't know what 4align='absmiddle' means, but we do know that a sine function with a period of 4 will be "none of the above."

It will be f(x) = sin(πx/2).

_____

The graph highlights one period of the function.