Part a)
At t = 0 the position of the object is given as
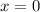
At t = 2
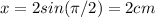
so displacement of the object is given as
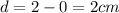
so average speed is given as
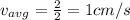
Part b)
instantaneous speed is given by


now at t= 0
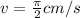
at t = 1
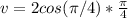
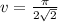
at t = 2
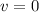
Part c)
Average acceleration is given as
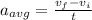
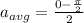
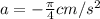
Part d)
Now for instantaneous acceleration
As we know that
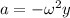
at t = 0
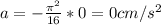
at t = 1
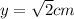
now we have
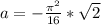
At t = 2 we have
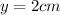
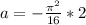
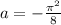
so above is the instantaneous accelerations