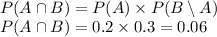When the occurrence of one event say A does not affect the occurrence of another event say B, than the two events are said to be independent such that;
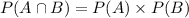
where, P(A) = probability of occurrence of event A
and P(B) = probability of occurrence of event B
(a).
Now, let event A = Sarah scores more than 175
and event B = Thomas scores more than 175
Thus, P(A)= Probability that Sarah scores more than 175 = 0.4
and P(B)= Probability that Thomas scores more than 175 = 0.2
Since, the scores are independent, thus the probability that both Sarah and Thomas scores more than 175 is,
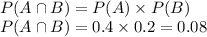
Hence, the required probability is 0.08
(b).
When the occurrence of one event say A affects the occurrence of another event say B, than the two events are said to be dependent such that;
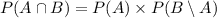
Now, let event A = Sarah scores more than 175
and event B = Thomas scores more than 175
Thus, P(A)= Probability that Sarah scores more than 175 = 0.4
P(B)= Probability that Thomas scores more than 175 = 0.2
and P(B|A) = Sarah scores more than Thomas given that Thomas scores more than 175 = 0.3
Thus, the required probability is calculated as follows;