Question

The bucket containing orange tennis balls and yellow tennis balls from which 5 balls are selected at random, but assume that the bucket contains 9 orange balls and 7 yellow balls. (1) what is the probability that, of the 5 balls selected at random, at least one is orange and at least one is yellow? (1) what is the probability that, of the 5 balls selected at random, at least two are orange and at least two are yellow?

Answer 1

(1)

Probability that all are yellow =
`(7*6*5*4*3)/(16*15*14*13*12)=0.0048`

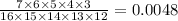
Probability that all are orange =
`(9*8*7*6*5)/(16*15*14*13*12)=0.0288`

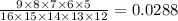
Sum of the two probabilities = 0048+ 0.0288=0.0336

Thus, the probability that at least one is orange and at least one is yellow = 1-0.0336= 0.9664= 96.64 %

(2) In addition to the above, we eliminate the "1 and 4" cases.

In these cases, any of the 5 can be taken out, so we multiply by 5.

1 yellow + 4 orange =
`5* ((7 * 9 * 8 * 7 * 6))/((16 * 15 * 14 * 13 *12))  = 0.2019`

1 orange + 4 yellow =
`5 * ((9 * 7* 6 * 5 * 4))/((16 * 15* 14 * 13 * 12)) = 0.0721`

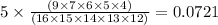
Sum of two probabilities = 0.2019+0.0721=0.2740

Now adding 0.0336 to this probability =0.0336+0.2740= 0.3076

Subtracting that from 1.0000 = 1-0.3076=0.6924= 69.24 %

Thus, the probability that, of the 5 balls selected at random, at least two are orange and at least two are yellow= 69.24%