Question

A particle moving along the x-axis has its velocity described by the function vx =2t2m/s, where t is in s. its initial position is x0 = 2.8 m at t0 = 0 s . at 1.3 s , what is the particle's position?

Answer 1

At time t = 1.3 s, the position of the particle is 4.3 m.

Velocity of a particle is the rate of change of its displacement.

Therefore, the velocity of the particle
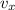`v_x` along the x direction is given by,

`v_x = (dx)/(dt)`

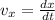
The change in the position of the particle is given by,

`dx = vdt`

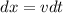
Integrate the equation.

`x=\int {v_x} \, dt`

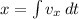
Substitute
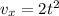`v_x =2t^2` and simplify.

`x=\int {v_x} \, dt =\int {2t^2} \, dt = (2)/(3) t^3+C`

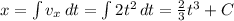
Calculate the constant of integration C by applying initial conditions, when t =0, x= 2.8 m.

`x=(2)/(3) t^3 + 2.8`

Substitute 1.3 s for t and calculate the value of x.

`x=(2)/(3) t^3 + 2.8\\ x_1_._3 =(2)/(3)(1.3)^3+2.8= 4.2647 m\\ =4.3 m (2 sf)`

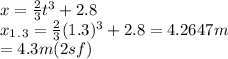
The position of the particle after 1.3 s is 4.3 m