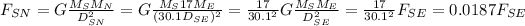Question

Neptune has a mass that is about 17 times the mass of Earth. The distance between the Sun and Neptune is about 30.1 times the distance between the Sun and Earth. If the gravitational force between the Sun and Earth is 3.5 x 1028 N, which is closest to the force between Neptune and the Sun?

Answer 1

Answer: 0.0187 times the force between Sun and Earth.

The gravitational force between two massive bodies is directly proportional to their masses and inversely proportional to the square of distance between them.

`F=G\frac {M_1M_2}{d^2}`

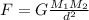
where G is the gravitational constant.

Let,

The mass of the Sun be
`M_S`

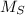
The mass of the Earth be
`M_E`

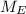
The mass of the Neptune be
`M_N`

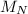
The Distance between Sun and Earth be
`d_(SE)`

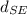
The Distance between Sun and Neptune be
`d_(NE)`

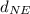
It is given that the mass of Neptune is 17 times mass of Earth.

`\Rightarrow M_N=17M_E`

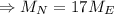
The distance of Neptune from Sun is 30.1 times the distance of Earth from Sun.

`\Rightarrow D_(SN)=30.1D_(SE)`

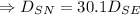
The Force between Earth and Sun is
`F_(SE)=3.5*10^(28)N`

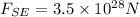
The Force between Neptune and Sun:

`F_(SN)=G(M_SM_N)/(D_(SN)^2)=G(M_S17M_E)/((30.1D_(SE))^2)=\frac {17}{30.1^2}G(M_SM_E)/(D_(SE)^2)=\frac {17}{30.1^2}F_(SE)=0.0187F_(SE)`

Answer 2

`F' = 6.57 * 10^(26) N`

Step-by-step explanation:

As we know that gravitational force of sun on earth is given as

`F = (Gm_1m_2)/(r^2)`

now we will have

`m_1` = mass of sun

`m_2` = mass of earth

so here force is given as

`F = 3.5 * 10^(28) N`

now we know that

mass of Neptune is 17 times mass of earth

`m_3 = 17m_2`

distance of Neptune from sun is 30.1 times the distance of Earth from sun

`r' = 30.1r`

so here the force between them is given as

`F' = (Gm_1m_3)/(r'^2)`

now we will have

`F' = (Gm_1(17m_2))/((30.1r)^2)`

`F' = (17)/((30.1)^2)F`

`F' = 0.0188F`

now plug in the value of force F

`F' = 0.0188* (3.5 * 10^(28))`

`F' = 6.57 * 10^(26) N`