Question

Verify that QT is Parallel to RS using the triangle proportionality theorem.

Answer 1

The triangle proportionality theorem is

If a line parallel to one side of a triangle intersects the other two sides of the triangle, then the line divides these two sides proportionally.

So to prove QT parallel to RS, we have to show

`(PQ)/(QR) = (PT)/(TS)`

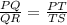
Substituting the values, we will get

`(18)/(38) = (36)/(80) \\ 0.47368421=0.45`

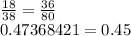
Which are not equal, therefore the lines are not parallel .