The value of n must be 2, so that both sides of the equation have the same dimensions.
Step-by-step explanation
The variables
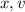 and
and
 have the dimensions of
have the dimensions of
![[l], ([l])/([t])](https://img.qammunity.org/2019/formulas/mathematics/college/7lks3t6lmvpnn19tz0vrz6v4j29osjnj00.png) and
and
![([l])/([t]^2)](https://img.qammunity.org/2019/formulas/mathematics/college/lr91y9w30ovwjtexnt4svcmdxvpqa3g9ae.png) respectively.
respectively.
These variables are related by an equation that has the form
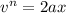
So, the dimension of the left side ⇒
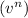 ⇒
⇒
![(([l])/([t]))^n](https://img.qammunity.org/2019/formulas/mathematics/college/thwh40g19yx0nwnygbzeonbt84xrlnmi0u.png)
and the dimension of the right side ⇒
 ⇒
⇒
![([l])/([t]^2) *[l]= ([l]^2)/([t]^2) = (([l])/([t]))^2](https://img.qammunity.org/2019/formulas/mathematics/college/u24ovi1t3kvlljtnt2lcwxacq4dy6l035a.png)
If both sides of the equation have the same dimensions, so...
![(([l])/([t]))^n = (([l])/([t]))^2\\ \\ So.. n= 2](https://img.qammunity.org/2019/formulas/mathematics/college/9eyz9kx89mf38en7r1n7nx2oaqjeyhq5l5.png)
So, the value of
 must be 2.
must be 2.