- Bicycles: 1 seat and 2 wheels
- Tricycles: 1 seat and 3 wheels
So with this, we will be making a system of equations. One representing the amount of seats and one representing the amount of wheels. Let x = bicycles and y = tricycles:
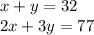
With this, I will be using the substitution method. Firstly, subtract y on both sides of the first equation:
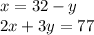
Next, substitute x in the second equation for (32 - y) and solve for y:
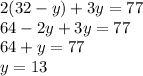
In short, there are 13 tricycles.