Answer:
The first system is consistent & dependent; the second system is inconsistent; and the third system is consistent & independent.
Explanation:
A consistent system is a system that has at least one solution. A dependent system is a system that has infinite solutions, because the equations describe the same line. An independent system is a system that has one solution.
An inconsistent system is a system that has no solution because the lines are parallel.
The first system is

To solve this, we would make the coefficients of y the same. We would do this by multiplying the top equation by 3:
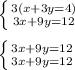
We have the same equation; thus this system is consistent and dependent.
The second system is
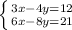
To solve this, we will make the coefficients of x the same; we will do this by multiplying the top equation by 2:
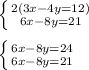
We have two equations that have the same slope but different y-intercepts; these lines are parallel and thus are inconsistent.
The third system is
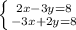
To solve this, we will make the coefficients of x the same; we will do this by multiplying the top equation by 3 and the bottom equation by 2:
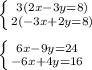
Now we will add the two equations:
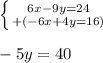
Divide both sides by -5:
-5y/-5 = 40/-5
y = -8
Now substitute this into the first equation:
2x-3(-8) = 8
2x+24 = 8
Subtract 24 from each side:
2x+24 - 24 = 8-24
2x = -16
Divide both sides by 2:
2x/2 = -16/2
x = -8
The solution is (-8, -8); thus the system is consistent and independent.