We can solve the problem by using conservation of momentum.
The player + ball system is an isolated system (there is no net force on it), therefore the total momentum must be conserved. Assuming the player is initially at rest with the ball, the total initial momentum is zero:

The total final momentum is:
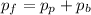
where
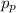 is the momentum of the player and
is the momentum of the player and
 is the momentum of the ball.
is the momentum of the ball.
The momentum of the ball is:
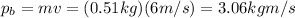
While the momentum of the player is:
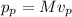 , where M=59 kg is the player's mass and vp is his velocity. Since momentum must be conserved,
, where M=59 kg is the player's mass and vp is his velocity. Since momentum must be conserved,
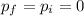
so we can write
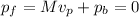
and we find

and the negative sign means that it is in the opposite direction of the ball.