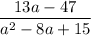First, we can bring both fractions under the common denominator (a - 3)(a - 5):
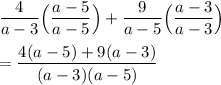
Looking at the numerator, we can distribute and collect like terms:
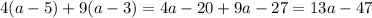
and looking at the denominator, we can do the same:
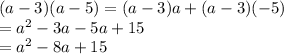
With these simplified expressions, the final fraction becomes