Question

One angle of a triangle has a measure of 66. The measure of the third angle is 57 more than half the measure of the second angle. The sum of the angle measures of a triangle is 180

Answer 1

So let's say that the second angle is x.

Then we can say that the third angle is
`(1)/(2)x+57`.

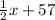So then we have three angles:

1) 66°

2) x°

3) (
`(1)/(2)x+57`)°

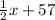So then we can add these together and solve for x by setting it equal to the total degrees left in the triangle after subtracting the known angle:

`x+(1)/(2)x+57=114`

`(3)/(2)x+57=114`

`(3)/(2)x=57`

`(2)/(3)*(3)/(2)x=57*(2)/(3)`

`x=(114)/(3) =38`

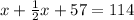
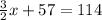
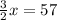
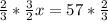
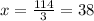
So now we know that the measure of the second angle is 38°. So then we can use this value to solve for the third angle:

`(1)/(2)(38) +57=76`

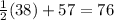
So the values of the angles are:

1) 66°

2) 38°

3) 76°