Given that a spinner with 3 sectors. The measures of the central angles of the red, white, and blue sectors, in that order, are in the ratio 2:3:4.
So we can write:
Measure of the central angle of the red sector = 2x
Measure of the central angle of the white sector = 3x
Measure of the central angle of the blue sector = 4x
We know that sum of central angle of the circle is 360 degree so the sum of above three angles will also be 360 degree
2x+3x+4x=360
9x=360
x=40
Then measure of the central angle of the red sector = 2x=2*40= 80 degree
Measure of the central angle of the white sector = 3x=3*40=120 degree
Measure of the central angle of the blue sector = 4x=4*40=160 degree
We have to find the probability for red sector so first we need to find are of the red sector which is given by formula :
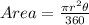 , where r is the radius of the spinner.
, where r is the radius of the spinner.
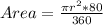
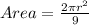
Area of the spinner is circular so that is given by
Area of spinner
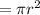
Now the probability that the arrow stops in the red sector is given by ratio or area of red sector and the area of spinner
Probability
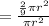
Probability
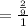
Probability

Hence required probability is 2/9.