Question

What is the simplified expression for,

3^negative 4 times 2^3 times 3^2 OVER 2^4 times 3^ negative 3?
THIS IS WRITTEN AS A FRACTION

3
-
2


3^2
______
2^2


3^2
_____
2


2^4
_____
3

Answer 1

Here are a few rules you need to know for this equation:

• Multiplying exponents of the same base:
  `x^m* x^n=x^(m+n)`
• Dividing exponents of the same base:
  `(x^m)/(x^n)=x^(m-n)`
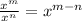
• Turning a negative exponent to a positive one:
  `x^(-m)=(1)/(x^m);(1)/(x^(-m))=x^m`

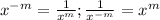
So this is our algebraic expression:
`(3^(-4)* 2^3* 3^2)/(2^4* 3^(-3))`

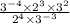
Firstly, multiply 3^-4 and 3^2:
`(3^(-4+2)* 2^3)/(2^4* 3^(-3))=(3^(-2)* 2^3)/(2^4* 3^(-3))`

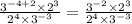
Next, divide:

`(3^(-2)* 2^3)/(2^4* 3^(-3))=3^(-2-(-3))2^(3-4)=3^12^(-1)`

Next, turn the negative exponent into a positive one:
`3^12^(-1)= (3)/(2)`

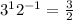
Your final answer is 3/2, or 1.5.