Question

Choose the abbreviation of the postulate or theorem that supports the conclusion that the triangles are congruent.

Given:
∠C, ∠F are rt. ∠'s; AB = DE; ∠A = ∠D

HL
LL
HA
LA

Answer 1

Answer: HA

Explanation:

Given: ∠C, ∠F are right angles ∠'s

Then the given triangles in picture Δ ABC and ΔDEF are right triangles, such that the sides opposite to the right angles AB and and DE are hypotenuse of triangles Δ ABC and ΔDEF respectively.

Also it is given that AB = DE; ∠A = ∠D

Then by HA theorem ,

Δ ABC ≅ ΔDEF

• HA Theorem says that if the hypotenuse and an angle of a right triangle are congruent to the hypotenuse and an angle of another triangle, then the two triangles are said to be congruent.

Answer 2

C. HA (Hypotenuse angle congruence).

Explanation:

We have been given a diagram of two right triangles. We are asked to choose the correct congruence theorem for our given triangles.

In our triangles ABC and DEF we have,

`m\angle C=m\angle F=90^o`

`AB=DE`

`\angle A=\angle D`

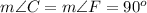
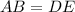
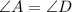
We can see that side length AB is hypotenuse of triangle ABC and side length DE is hypotenuse of triangle DEF.

Angle A and angle D are acute angles (less than 90 degrees) as we have one right angle in our both triangles and measure of other two angles will be 90 degrees in both triangles by angle sum property of triangles.

Hypotenuse angle theorem states that two right triangles are congruent, if the hypotenuse and an acute angle of one right triangle are congruent to the hypotenuse and an acute angle of another right triangle.

Therefore, by HA congruence triangle ABC is congruent to triangle DEF and option C is the correct choice.