Answer:
Option C. 4.8 units
Explanation:
In the given figure side AB = 8.6
Coordinates of A(1, 3), B(8, 8), C(12, 5) and D(5, 0)
Now in the given triangle we will find the angle between Ab and AD to find the length of AE which is the length of the given parallelogram.
tanθ =
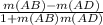
Slope m(AB) =
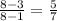
Slope m(AD) =

So tanθ =
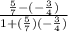
tanθ =
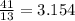
θ =
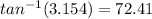 °
°
Now in right angle triangle ABE
sin72.41° =

.95324 =

DE = 5×4.7662 = 4.8 units
Option C is the answer.