For the greatest total area, length will be 120 ft. and width will be 80 ft.
Explanation
Lets assume, the length of the playground is
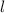 ft. and width is
ft. and width is
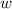 ft.
ft.
Suppose, the playground is divided into two parts by a fence parallel to width. That means the length of the divider fence will be
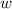 ft.
ft.
So, the total length of the fence needed
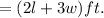
It is given in the question that 480 feet of fencing is used. That means...
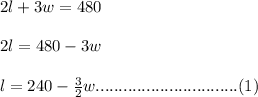
Now, the area of the playground....
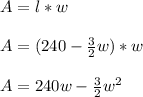
Taking derivative on both side in respect of
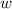 , we will get...
, we will get...
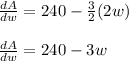
A will be maximum when
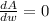 . That means...
. That means...

Now plugging this
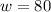 into equation (1)...
into equation (1)...
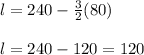
So, for the greatest total area, length will be 120 ft. and width will be 80 ft.