Question

Find the values of x and y for 3x + 2iy = 6 + 10i

Answer 1

Answer: The required values are x = 2 and y = 5.

Step-by-step explanation: We are given to find the values of x and y from the following equation :

`3x+2iy=6+10i~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

To find the values of x and y from the given equation, we need to compare the real and imaginary parts of the equation.

After comparing the real and imaginary parts from both sides of equation (i), we get

`3x=6\\\\\Rightarrow x=(6)/(3)\\\\\Rightarrow x=2`

and

`2y=10\\\\\Rightarrow y=(10)/(2)\\\\\Rightarrow y=5.`

Thus, the required values are x = 2 and y = 5.

Answer 2

In this question, the given equation is

`3x + 2yi = 6 + 10i`

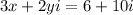
To solve for x and y, we have to compare both sides, and on doing so, we will get

`3x=6, 2y=10`

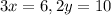
Now we need to isolate x and y, by getting rid of 3 and 2 , that is with x and y respectively .

`x=2, y=5`

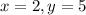
So for the given equation to be true, the values of x and y are 2 and 5 respectively .