Question

If there are more than two numbers in a certain list, is each of the numbers in the list equal to 0 ? (1) the product of any two numbers in the list is equal to 0. (2) the sum of any two numbers in the list is equal to 0.

Answer 1

If the product of any two numbers in the list is equal to 0, you can't conclude that the list is composed only by zeroes. In fact, suppose that you have a list of N numbers which are all zeroes except one:

`x_1 = x_2 = \ldots = x_(N-1) = 0,\ x_N = k\\eq 0`

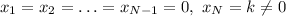
Whenever you multiply two elements of this list, you either multiplies two zeroes, or you multiply the non-zero element by a zero element, and so the result is zero, but the list is not composed by zeroes only.

If instead the sum of any two numbers in the list is equal to 0, you can conclude that the list is composed by zeroes only.

NOTE: if you allow a number to be multiplied by itself, then both answers would be good! So, the complete answer is:

If you cannot use the same number twice: condition (1) is not sufficient, condition (2) is sufficient to say that the list constains only zeroes

If you can use the same number twice: both conditions are sufficient to say that the list constains only zeroes