Volume of the peat moss =

=
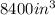
Convert the above volume into
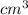
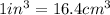
Thus, volume in
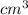 is:
is:
Volume of peat moss =

=
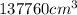
Now,
Total volume by using area and depth of the peat moss =
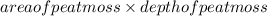
=
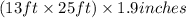
=

Convert above values in
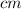 to get the value of volume in
to get the value of volume in
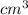 :
:
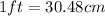
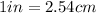
Thus, volume in
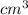 is:
is:
Total volume =
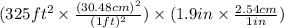
=
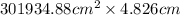
=
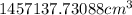
Now, number of bags is calculated by the ratio of total volume of the peat moss to the volume of the peat moss.
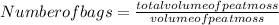
Substitute the values of volume in above formula:
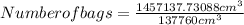
=
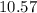
≅
 bags
bags
Thus, number of bags of peat moss are needed to cover an area measure
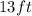 by
by
 to a depth of
to a depth of
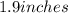 are
are
 bags.
bags.