Question

The distribution of the amount of money spent by first-time gamblers at a major casino in las vegas is approximately normal in shape with a mean of 600 a n d a s t a n d a r d d e v i a t i o n o f 120. according to the standard deviation rule, almost 84% of gamblers spent more than what amount of money at this casino?

Answer 1

Solution: We are given:

`\mu=600, \sigma =120`

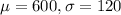
We need to find the z value corresponding to probability 0.84, in order to find the how much money almost 84% of gamblers spent at casino.

Using the standard normal table, we have:

`z(0.85) = 0.9945`

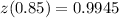
Now we will use the z score formula to find the required amount:

`z=(x-\mu)/(\sigma)`

`0.9945=(x-600)/(120)`

`0.9945 * 120 = x - 600`

`119.34 = x - 600`

`x = 600 + 119.34`

`x = 719.34`

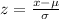
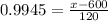
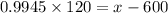
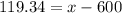
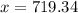
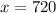`x = 720` approximately

Therefore, almost 84% of gamblers spent more than $720 amount of money at this casino.