Question

When 108 g of water at a temperature of 23.9 °c is mixed with 66.9 g of water at an unknown temperature, the final temperature of the resulting mixture is 47.2 °c. what was the initial temperature of the second sample of water? (the specific heat capacity of liquid water is 4.184 j/g ⋅ k.)?

Answer 1

Here,

Heat gain by the first sample of water + Heat lost by the second sample of water is equal to zero (0).

Now, Mass of water sample one = 108 g (given)

Mass of water sample two = 66.9 g (given)

Temperature for water sample one =
`23.9^(0)C`

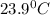
Let, temperature for water sample two =x

And, final temperature =
`47.2^(0)C`

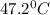
Now,

`mass of water sample one* specific heat of water* (T_(f) - T_(i)) + mass water sample two* specific heat of water* (T_(f) - T_(i)) = 0`

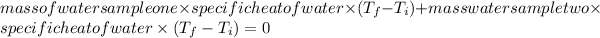
where,
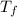`T_(f)` = final temperature

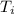`T_(i)` = initial temperature

Substitute all the given values in above formula:

`(108 g* 4.184 J/g . K* ( 47.2^(0)C- 23.9^(0)C) )+ (66.9 g * 4.184 J/g . K* (47.2^(0)C -x))= 0`

`(451.872 J/K * (23.3^(0)C)) + (279.9096 J/K* (47.2^(0)C -x)) = 0`

`(10528.6176 J/K(^(0)C)+ (13211.73312 J/K(^(0)C) -279.9096 J/K* x)= 0`

`(23740.35072 J/K(^(0)C) -279.9096 J/K* x)= 0`

`-279.9096 J/K* x= -23740.35072 J/K(^(0)C)`

`x =(23740.35072 J/K(^(0)C))/(279.9096 J/K)`

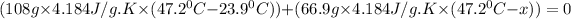
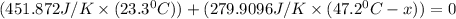
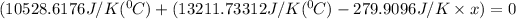
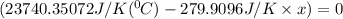
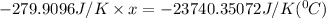
[tex x =84.81^{0}C [/tex]