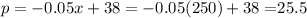Question

Suppose that when the price of a certain commodity is p dollars per unit, then x hundred units will be purchased by consumers, where p 0.05x 38. the cost of producing x hundred units is c(x) 0.02x 2 3x 574.77 hundred dollars. sobecki, dave; price, michael; hoffmann, laurence; bradley, gerald. applied calculus for business, economics, and the social and life sciences, expanded edition, 11th edition (page 28). mcgraw-hill higher education -a. kindle edition.

Answer 1

`Profit = TR- TC = x (P) - C(x) = x(-0.05x+38) - (0.02x^(2) + 3x + 574.77) = -0.05x^(2) + 38x - 0.02x^(2) - 3x - 574.77 = -0.07x^(2) + 35x -574.77`

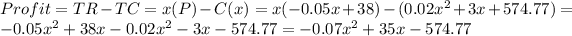
This profit equation is an equation of a parabola that opens downward (Since A=-0.07<0) and has its vertex at

`x= -(B)/(2A)  = -(35)/(2 (-0.07))  = 250`

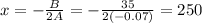
Thus, revenue is maximized when x=250 hundred units. At this quantity maximum profit is

P(250)=3800.23 hundred dollars

b. Profits are maximised at x=250 hundred units. The per unit price at this is,

`p= -0.05x + 38 = -0.05 (250) + 38 = $25.5`