Answer:
118 degrees.
Explanation:
Let x represent measure of base angle.
We have been given that the measure of vertex angle in an isosceles triangle is six less than four times the measure of base angle.
Four times measure of base angle would be
 .
.
Six less than four times the measure of a base angle would be
 .
.
We know that base angles of an isosceles triangle are equal and measure of all angles of a triangle is 180 degrees.
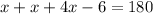

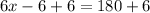
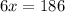
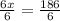
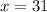
Now, we will substitute
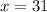 in expression
in expression
 to find the measure of vertex angle.
to find the measure of vertex angle.
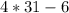
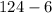
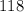
Therefore, the measure of vertex angle is 118 degrees.