Question

the measure of the vertex angle in an isosceles triangle is six less than four times the measure of a base angle find the measure of the vertex angle

Answer 1

118 degrees.

Explanation:

Let x represent measure of base angle.

We have been given that the measure of vertex angle in an isosceles triangle is six less than four times the measure of base angle.

Four times measure of base angle would be
`4x`.

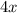Six less than four times the measure of a base angle would be
`4x-6`.

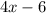We know that base angles of an isosceles triangle are equal and measure of all angles of a triangle is 180 degrees.

`x+x+4x-6=180`

`6x-6=180`

`6x-6+6=180+6`

`6x=186`

`(6x)/(6)=(186)/(6)`

`x=31`

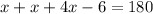
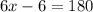
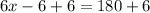
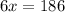
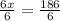
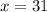
Now, we will substitute
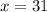`x=31` in expression
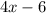`4x-6` to find the measure of vertex angle.

`4*31-6`

`124-6`

`118`

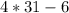
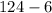
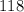
Therefore, the measure of vertex angle is 118 degrees.

Answer 2

Base angle: x

Vertex angle: 4x - 6

In an isosceles triangle, the base angles are equal. The sum of the angles of a triangle equal 180°

Base angle + Base angle + vertex angle = 180°

x + x + 4x - 6 = 180

6x - 6 = 180

6x = 186

x = 31

Vertex angle: 4x - 6 = 4(31) - 6 = 124 - 6 = 118

Answer: 118°