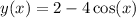The general solutions always have some additive/multiplicative constant, that you must fix in the particular solution.
In order to do so, you need to impose that the particular solution passes through a certain point. In your case, you have
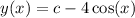
and you want

Put everything together, and you have

Since the cosine is zero in the chosen point. So, we've fixed the value of the constant, and the particular solution is found: