Question

For what values of b are the vectors ⟨−110,b,10⟩ and ⟨b,b2,b⟩ orthogonal?

Answer 1

Two vectors are orthogonal if their dot product is zero. The dot product is the sum of the multiplications of entries with same index:

`(a,b,c) \cdot (d,e,f) = ad+be+cf`.

So, in your case,

`(-110,b,10) \cdot (b,b^2,b) = -110b+b^3+10b = b^3-100b`

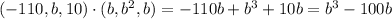
So, the two vectors are orthogonal if and only if

`b^3-100b = 0 \iff b(b^2-100) = 0 \iff b=0 \lor b^2-100=0 \iff b = 0 \lor b = \pm 10`

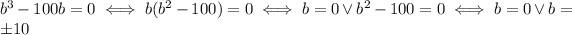
The solution
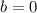`b=0` is indeed trivial: in that case, the second vector is the null vector, which is orthogonal to every possible vector.