Question

Let y′′′−9y′′+20y′=0. find all values of r such that y=erx satisfies the differential equation. if there is more than one correct answer, enter your answers as a comma separated list.

Answer 1

we are given

differential equation as

`y'''-9y''+20y'=0`

we are given

`y=e^(rx)`

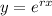
Firstly, we will find y' , y'' and y'''

those are first , second and third derivative

First derivative is

`y'=re^(rx)`

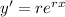
Second derivative is

`y''=r*re^(rx)`

`y''=r^2e^(rx)`

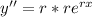
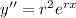
Third derivative is

`y'''=r^2*re^(rx)`

`y'''=r^3e^(rx)`

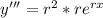
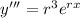
now, we can plug these values into differential equation

and we get

`r^3 e^(rx)-9r^2 e^(rx)+20re^(rx)=0`

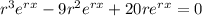
now, we can factor out common terms

`e^(rx)(r^3 -9r^2 +20r)=0`

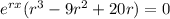
we can move that term on right side

`(r^3 -9r^2 +20r)=0`

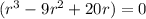
now, we can factor out

`r(r^2 -9r +20)=0`

`r(r-5)(r-4)=0`

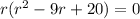
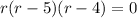
now, we can set them equal

`r=0`

`r-5=0`

`r=5`

`r-4=0`

`r=4`

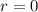
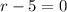
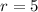
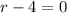
so, we will get

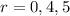`r=0,4,5`...............Answer