Solution: A distribution consists of three components with frequencies 45 ,40 and 15 having their means 2,2.5 and 2 respectively . find combined mean
Answer: Let
 be the mean of first component and
be the mean of first component and
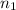 be the frequency of first component
be the frequency of first component
Let
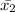 be the mean of second component and
be the mean of second component and
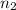 be the frequency of second component
be the frequency of second component
Let
 be the mean of third component and
be the mean of third component and
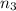 be the frequency of third component
be the frequency of third component
Then we have:
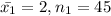
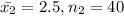
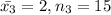
Now the combined mean is:
Combined mean

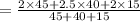
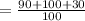
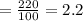
Therefore, the combined mean is 2.2