Question

Chris measures the angle of elevation to the top of a building as 38°. When Chris moves 100 ft closer to the base of the building, the angle of elevation to the top of the building is 47°. How tall is the building? Neglect Chris' height and round your answer to the nearest tenth of a foot.

Answer 1

Call x the distance on the ground to the base of the building for the first measurement of 38°. Call the height of the building is y.

The height is the opposite of the angle, for each angle, so related to the adjacent side through the tangent.

`y = x \tan 38^\circ`

`y = (x- 100) \tan 47^\circ`

`x \tan 38^\circ = x \tan 47^\circ - 100 \tan 47^\circ`

`100 \tan 47^\circ = x(\tan 47^\circ - \tan 38^\circ)`

`x = (100 \tan 47^\circ)/(\tan 47^\circ - \tan 38^\circ)`

`y = x \tan 38^\circ = (100 \tan 47^\circ \tan 38^\circ)/(\tan 47^\circ - \tan 38^\circ)`

`y \approx 287.83`

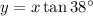
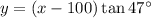
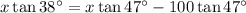
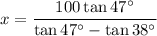
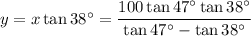
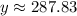
Answer: 287.8 feet