Question

Find the coordinates of the points of trisection of the line segment joining the points (3, – 2) and (– 3, – 4).

Answer 1

Let us suppose the given points are A (3, – 2) and B(– 3, – 4).

Let P and Q be the point of trisection. Therefore, we have

`AP=PQ=QB`

Trisection means is to divide a line segment into three equal parts. Hence, we can say that P divides AB in the ratio of 1:2 and Q divides in 2:1 .

Thus, coordinate of P is given by

`P=((mx_2+nx_1)/(m+n) ,(my_2+ny_1)/(m+n))\\ \\ P=((1* (-3)+2* 3)/(1+2) , (1* (-4)+2* (-2))/(1+2) )\\ \\ P=((-3+6)/(3) ,(-8)/(3) )\\ \\ P=(1,-(8)/(3) )`

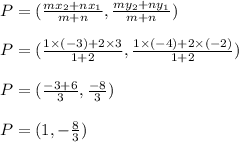
Similarly the coordinate of Q is given by

`Q=((2* (-3)+1* 3)/(1+2) , (2* (-4)+1* (-2))/(2+1) )\\ \\ Q=\left ((-6+3)/(3),(-8-2)/(3)  \right )\\ \\ Q=\left ( (-3)/(3),-(10)/(3) \right )\\ \\ Q=\left ( -1,-(10)/(3) \right )`

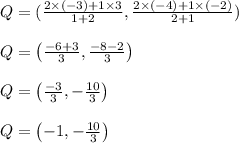
Therefore, the coordinates of the point of trisection are

`(1,-(-8)/(3))\text{ and }\left ( -1,-(10)/(3) \right )`