Question

Determine if the following equations form a perpendicular line or not

Answer 1

• Slope-Intercept Form: y = mx + b, with m = slope and b = y-intercept.

If two lines are perpendicular, then they will have slopes that are negative reciprocals to each other. An example of negative reciprocals are 2 and -1/2

6.

Now with line 2, I have to convert it to slope intercept form. Firstly, subtract 2x on both sides of the equation:
`-5y=-2x+8`

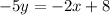
Next, divide both sides by -5 and your slope-intercept form is
`y=(2)/(5)x+(8)/(5)`

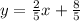
Now since 2/5 is not the negative reciprocal of -2/5, these lines are not perpendicular.

7.

It's pretty much the same process; convert to slope-intercept and determine if negative reciprocal. This time I'll brush through them:

`6x-3y=15 \\-3y=-6x+15\\y=2x-5\\\\2x+4y=-12\\4y=-2x-12\\y=-(1)/(2)x-3`

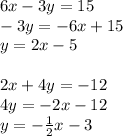
Now since 2 is the negative reciprocal of -1/2, these lines are perpendicular.