Question

Find the length of the arc in terms of pi. Help please!

Answer 1

For this problem, we will need to use the formula for arc length, which is
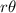`r\theta`, where
`r` is the radius of the circle and
`\theta` is the central angle in radians.

We can clearly see that the radius of the circle is 8. However, no central angle is given to us. However, we can see that the measure of arc AB is 45°. This means that the central angle of arc AB is also 45°. (Remember that the measure of arc is the same as the measure of its central angle.) Converting 45° to radians, we get
`(\pi)/(4)`.

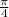We can now plug this information into the formula to find our answer:

`8((\pi)/(4)) = \boxed{2\pi}`

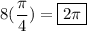
The answer is 2π.

Answer 2

arc length (s) = radius (r) · angle (θ) (the angle must be in radians!)

45° =
`(\pi)/(4)`

s = 8 ·
`(\pi)/(4)`

=
`(8\pi)/(4)`

= 2π

Answer: 2π