Question

The triangles below are similar. Find x showing the proportion and all work.

Answer 1

we are given that

two triangles are similar

so, the ratio of their sides must be same

we get

`(2)/(6) =(x)/(x+2)`

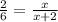
now, we can solve for x

step-1: Cross multiply both sides

`2(x+2) =6x`

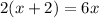
step-2: Simplify left side

`2x +4 =6x`

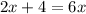
step-3: Subtract both sides by 2x

`2x +4-2x =6x-2x`

`4 =4x`

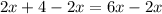
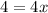
step-4: Divide both sides by 4

`x=1`

so,

`x=1`............Answer