The composed fraction
 means that the input of
means that the input of
 is the ouput of
is the ouput of
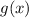 .
.
So, the chain is

The domain of
 is composed by all inputs which are not zero, otherwise we would have a zero denominator.
is composed by all inputs which are not zero, otherwise we would have a zero denominator.
So, since
 doesn't accept 0 as an input, and we want to feed it with
doesn't accept 0 as an input, and we want to feed it with
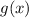 , we conclude that
, we conclude that
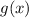 can't be zero.
can't be zero.
So, we have
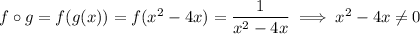
Since
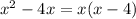
we have
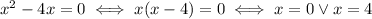
Since these two points cases
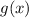 to vanish, they can't be accepted as inputs by
to vanish, they can't be accepted as inputs by
 .
.