So let's set the variables:
Nate: x
Bryan: x + 150
Cameron 2(x + 150)
If the total amount of papers delivered was 1450, we can then set all of this equal to 1450 and solve for x:
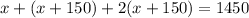
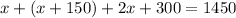
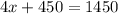
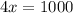
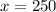
So now we can solve for how many papers each child delivered:
Nate: 250
Bryan: (x + 150) = 250 + 150 = 400
Cameron: 2(x + 150) = 2(250 + 150) = 2(400) = 800