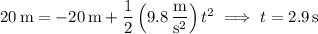Take the first coconut's starting position to be the origin, and the downward direction to be positive. The first coconut's position is determined by
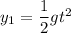
where
 is the acceleration due to gravity.
is the acceleration due to gravity.
So if it takes 2.0 s to reach the ground, then
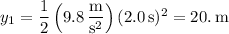
(rounding to 2 significant digits)
The second coconut starts 20 m higher than the first, so its initial displacement is -20 m relative to the origin, and its overall position over time is given by
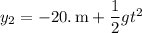
Reaching the ground is a matter of obtaining
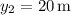 , which requires a time of
, which requires a time of