Question

A circle has a radius of \sqrt{37} 37 ​ square root of, 37, end square root units and is centered at (1.3,-3.5)(1.3,−3.5)left parenthesis, 1, point, 3, comma, minus, 3, point, 5, right parenthesis. write the equation of this circle.

Answer 1

General form of the equation of a circle is

( x - a)^2 + (y - b)^2 = r^2 where (a, b) is the centre and r = radius

So here it is (x - 1.3)^2 + (y - (-3.5))^2 = ( √37)^2

= (x - 1.3)^2 + (y + 3.5)^2 = 37 answer

Answer 2

`(x-1.3)^2+(y+3.5)^2=37`

Explanation:

We have been given that a circle has a radius of
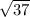`√(37)` units and is centered at
`(1.3,-3.5)`. We are asked to write an equation for our given circle.

We know that standard form of a circle is in form
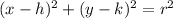`(x-h)^2+(y-k)^2=r^2`, where,

(h,k) = Center of circle,

r = Radius of circle.

Upon substituting our given values in circle equation, we will get:

`(x-1.3)^2+(y--3.5)^2=(√(37))^2`

`(x-1.3)^2+(y+3.5)^2=37`

Therefore, our required equation would be
`(x-1.3)^2+(y+3.5)^2=37`.