Question

Triangle $abc$ has vertices at $a(5,8)$, $b(3,-2)$, and $c(6,1)$. the point $d$ with coordinates $(m,n)$ is chosen inside the triangle so that the three small triangles $abd$, $acd$ and $bcd$ all have equal areas. what is the value of $10m + n$?

Answer 1

10m + n = 49

Step-by-step explanation:

Point D will be the centroid of ABC. To find the centroid we use formula.

Given the coordinates of the three vertices of a triangle ABC,

the centroid D coordinates are given by -

m = (x₁ + x₂ + x₃)/3 & n = (y₁ + y₂ + y₃)/3

m =
`(5 + 3 + 6)/(3)`

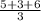
m =
`(14)/(3)`

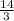
and

n =
`(8-2+1)/(3)`

n =
`(7)/(3)`

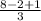
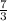
Now we will find the value of 10m+n

=
`10*(14)/(3) + (7)/(3)`

=
`(140)/(3) + (7)/(3)`

`= (147)/(3)`

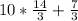
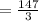
= 49

So, 10m + n = 49

That's the final answer.