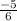Question

Determine a constant $k$ such that the polynomial $$ p(x, y, z) = x^5 + y^5 + z^5 + k(x^3+y^3+z^3)(x^2+y^2+z^2) $$ is divisible by $x+y+z$.

Answer 1

k =
`(-5)/(6)`

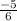
Step-by-step explanation:

If we assume such a constant exists, then we can solve for it by setting up an equation based on

P(x,y,z)=0

whenever

x+y+z=0.

For example, P(2,-1,-1)=0.

Now we put x = 2, y = -1, z=-1

p(x, y, z) = x⁵ + y⁵ + z⁵ + k(x³+y³+z³)(x²+y²+z²)

p(2,-1,-1) = 2⁵ + (-1)⁵+ (-1)⁵ + k(2³ + (-1)³+ (-1)³)(2² + (-1)²+ (-1)²)

0 = 32 - 1 -1 + k(8-1-1)(4+1+1)

0 = 30 + k(6)(6)

0 = 30 + 36k

solve for k

k =
`(-30)/(36)`

k =
`(-5)/(6)`