Question

If a 5 cm piece of wire is cut into two parts such that a square formed by bending one part will have four times the area of a square formed by bending the other part, what is the length of the longer part

Answer 1

Let the length of one part of a wire be 'x' cm.

The length of the remaining part of the wire is '5-x' cm.

Since, square formed by bending one part will have four times the area of a square formed by bending the other part.

Area of square formed by the length of one part =
`(Side)^2`

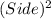
Therefore, Area of square formed by the length of one part =
`(x)^2`

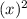
Area of square formed by the length of other(remaining) part =
`(5-x)^2`

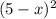
According to the question,

`(x)^2` =
`4(5-x)^2`

`x^2 = 4(25+x^2-10x)`

`x^2 = 100+4x^2-40x`

`3x^2-40x+100=0`

`3x^2-30x-10x+100=0`

`3x(x-10)-10(x-10)=0`

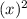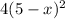
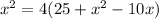
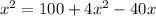
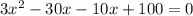
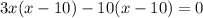
x = 10 or
`x = (10)/(3)`

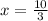
Since length of the wire was 5 cm. So, 10 cm is not possible.

Therefore, the length of one part of the wire =
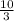`(10)/(3)`cm.

Therefore, the length of other part of the wire =
`5 - (10)/(3)`

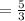`= (5)/(3)`cm.