1) First, remember that 2 pairs of adjacent sides are congruent for kites. Since BD is showing 2 different lengths at their intersection from AC, then the congruent sides must be AB ≡ BC and CD ≡ DA.
2) Next, you need to remember how to find the perimeter (P). It is the sum of the outside side lengths. P = AB + BC + CD + DA.
3) Lastly, you need to remember that the diagonals of a kite are perpendicular, which means that you can use the Pythagorean Theorem to find the lengths of the hypotenuse. In this case, the hypotenuse is the outside side length.
4) Now you can use these tools to solve!
AC = 48. Since we don't know at what distance it intersects BD, let's use 48-x to represent one side and "x" to represent the other side.
For convenience, let's consider the intersection of the diagonals point "O"
Triangle AOB: (48-x)² + 18² = AB Triangle COB: (x)² + 18² = BC
Since AB = BC you can use substitution to set the equations equal to each other. (48-x)² + 18² = (x)² + 18² Solve to find that x = 24 and 48 - x = 24
Now use the Pythagorean Theorem to find AB (which equals BC)
AB =
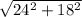 =
=
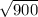 = 30
= 30
Do the same to find CD (which equals DA)
CD =
 =
=
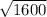 = 40
= 40
Finally, you have enough information to find the perimeter: P = AB + BC + CD + DA → P = 30 + 30 + 40 + 40 → P = 140
Answer: 140 m