Question

Find the missing b for a trapezoid with a=68, h=4, b=21

Answer 1

We will have to use the formula for the area of a trapezoid on this problem, which is (
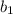`b_1` and
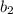`b_2` are the bases of the trapezoid and
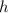`h` is the height):

`(b_1 + b_2)/(2) \cdot h`

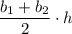
All we need to do is substitute the information we are given into our formula:

`(21 + b_2)/(2) \cdot 4 = 68`

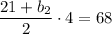
Now, let's just simplify the equation:

`(21 + b_2)/(2) \cdot 4 = 68`

`(21 + b_2)/(2) = 17`

`21 + b_2 = 34`

`b_2 = 13`

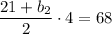
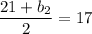
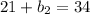
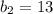
The missing base has a length of 13 units.