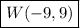Question

How to solve and the answer?

Answer 1

For both of these problems, we are going to need to use our midpoint formula (the formula uses the coordinates
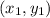`(x_1, y_1)` and
`(x_2, y_2)`):

`\Bigg((x_1 + x_2)/(2) , (y_1 + y_2)/(2)\Bigg)`

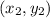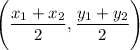
Problem 9:

Let's insert use the information we already know to create an equation which we can solve:

`\Bigg((6 + x_2)/(2), (0 + y_2)/(2)\Bigg) = (-3, 2)`

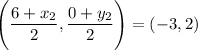
Now, let's solve the x-value and y-value of the coordinate independently:

`(6 + x_2)/(2) = -3 \Rightarrow 6 + x_2 = -6 \Rightarrow x_2 = -12`

`(y_2)/(2) = 2 \Rightarrow y_2 = 4`

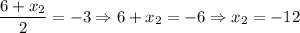
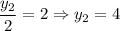
We have found both the x-value and y-value of
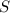`S`, making the final answer:

`\boxed{S(-12, 4)}`

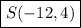
Problem 10:

We are going to do the same process as Problem 9.

`\Bigg((7 + x_2)/(2) , (1 + y_2)/(2)\Bigg) = (-1, 5)`

`(7 + x_2)/(2) = -1 \Rightarrow 7 + x_2 = -2 \Rightarrow x_2 = -9`

`image`

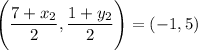
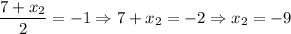
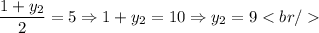
Our answer is:

`\boxed{W(-9, 9)}`