Question

How does the distance formula ensure that the distance between two different points is positive?

Answer 1

Since the distance formula is square rooted, one of the number one things that will never ever happen in math... the square root a negative number. Try it in your calculator it will say ERROR.

Answer 2

`(x_(2)-x_(1) ) ^(2) \geq 0 , always\\(y_(2)-y_(1) ) ^(2) \geq 0 , always\\so, \\\sqrt{(x_(2)-x_(1) ) ^(2) +(y_(2)-y\\_(1) ) ^(2) } \geq 0, always`

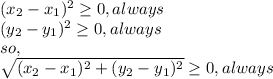
Explanation:

Hello, I can help you with this. I like this kind of questions.

Step one

Let's remember the formula

Let

`P1(x_(1), y_(1))\\P2(x_(2), y_(2))\\`

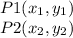
the distance between P1 and P2 is given by:

`Distance=\sqrt{(x_(2)-x_(1)) ^(2)+(y_(2)-y_(1))^(2) }`

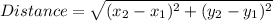
as you can see, the terms are powered to 2, so it does not matter the sign, it always will be positive

`(x_(2)-x_(1) ) ^(2) \geq 0 , always\\(y_(2)-y_(1) ) ^(2) \geq 0 , always\\so, \\\sqrt{(x_(2)-x_(1) ) ^(2) +(y_(2)-y\\_(1) ) ^(2) } \geq 0, always`

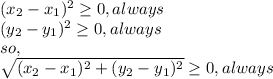
I really hope it helps, have a nice day