Question

PLEASE HELP!!! For the function f(x)=  -4√x - 1

, find the inverse function

Answer 1

1. B

2.D

3.B

4.A

Explanation:

100%

Answer 2

as you already know, to get the inverse of any expression, we start off by doing a quick switch on the variables, and then solve for y.

`\bf \stackrel{f(x)}{y}=-4√(x-1)\implies \stackrel{\textit{quick switcheroo}}{\underline{x}=-4\sqrt{\underline{y}-1}}\implies \cfrac{x}{-4}=√(y-1)\\\\\\\stackrel{\textit{squaring both sides}}{\left( -\cfrac{x}{4} \right)^2=(√(y-1))^2}\implies \cfrac{x^2}{16}=y-1\implies \cfrac{x^2}{16}+1=\stackrel{f^(-1)(x)}{y}`

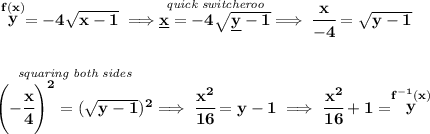
for that inverse to be a function, it has to be a one-to-one function, and that can only happen if it can pass the horizontal and vertical lines tests, and that can only be if x ⩽ 0, check the picture below.