A set of data has a normal distribution with a mean of 5.1 and a standard deviation of 0.9. Find the percent of data between 4.2 and 5.1. A)about 68% B)about 34% C)about 16% D)a…

Question

asked Aug 8, 2019 158k views

2 Answers

Rei · Answer 1 · 2019-08-14T01:12:52+0000

A set of data has a normal distribution with a mean of 5.1 and a standard deviation of 0.9. Find the percent of data between 4.2 and 5.1.

Answer: The correct option is B) about 34%

Proof:

We have to find
P(4.2<x<5.1)

To find
P(4.2<x<5.1) , we need to use z score formula:

When x = 4.2, we have:

$z = (x-\mu)/(\sigma)$

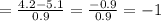
=(4.2-5.1)/(0.9)=(-0.9)/(0.9)=-1

When x = 5.1, we have:

$z = (x-\mu)/(\sigma)$

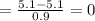
=(5.1-5.1)/(0.9)=0

Therefore, we have to find
P(-1<z<0)

Using the standard normal table, we have:

P(-1<z<0) =
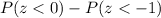
P(z<0) - P(z<-1)

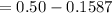
=0.50-0.1587

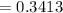=0.3413 or 34.13%

= 34% approximately

Therefore, the percent of data between 4.2 and 5.1 is about 34%