Question

Analyze the diagram below and complete the instructions that follow. Find the values of x and y. Using those values, explain what is wrong with the figure above.

Answer 1

The value of x is 12 and the value of y is 23. The given figure wrong because the vertically opposite angles are not same.

Explanation:

From the given graph it is clear that lines XY and WZ intersect each other at point A and make 4 angles.

The angle XAZ and angle ZAY are supplementary angles because they lie on a straight line.

`\angle XAZ+\angle ZAY=180`

`6x+35+8x-23=180`

`14x+12=180`

`14x=168`

`x=12`

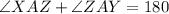
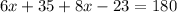
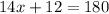
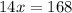
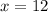
The value of x is 12.

The angle XAW and angle WAY are supplementary angles because they lie on a straight line.

`\angle XAW+\angle WAY=180`

`3y+y+88=180`

`4y+88=180`

`4y=92`

`y=23`

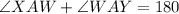
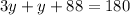
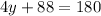
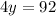
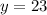
The value of y is 23.

The value of x is 12 and the value of y is 23, so the measure of all angles are

`\angle XAZ=6x+35=6(12)+35=107`

`\angle ZAY=8x-23=8(12)-23=73`

`\angle XAW=3y=3(23)=69`

`\angle WAY=y+88=23+88=111`

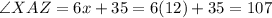
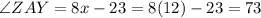
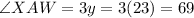
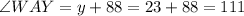
If two line intersect each other then the vertically opposite angles are always same. But here vertically opposite angles are not same.

`\angle XAZ\\eq \angle WAY`

`\angle ZAY\\eq \angle XAW`

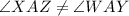
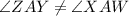
Therefore the given figure wrong because the vertically opposite angles are not same.